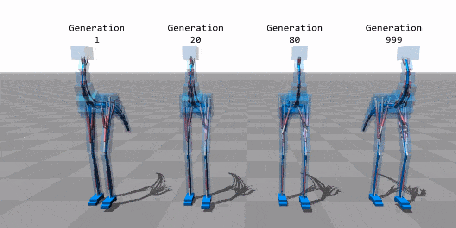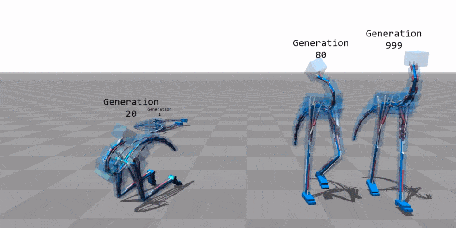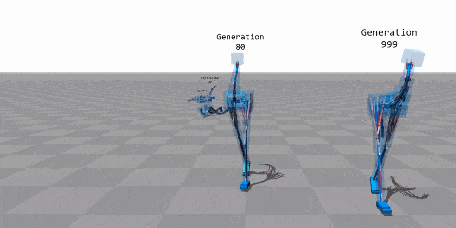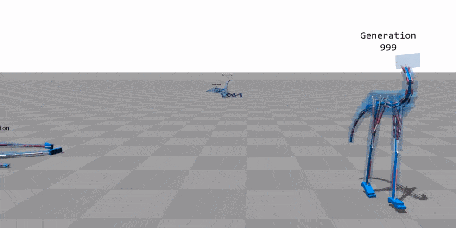
When Biology Meets Data Science—An Introduction to Neuroevolution¶
Tim Hargreaves
PyData Manchester
23rd June 2020
Introduction¶
About Me¶
- MathStat Undergraduate at University of Warwick
- Data Scientist at AstraZeneca
- Computational Statistics and Machine Learning
Format¶
- High-level with links to further reading
- Source code/presentation will be linked at the end
- Chance for Q&As after talk
Motivation¶
Conventional Methods for Designing/Tuning Neural Networks¶
| Method | Flaws |
|---|---|
| Copy someone else | Requires trust/might not be appropriate |
| Use intuition | No reproducibility; requires said intuition |
| Brute force/random search | Computational complexity |
| Gradient-based methods | Lack of convexity; non-differentiable hyperparameters |
| Bayesian methods | Deciding priors/measuring convergence can be difficult |
A Contrasting Approach¶
- Evolution offers a solution
- Can we implement something similar?
Evolutionary Algorithms¶
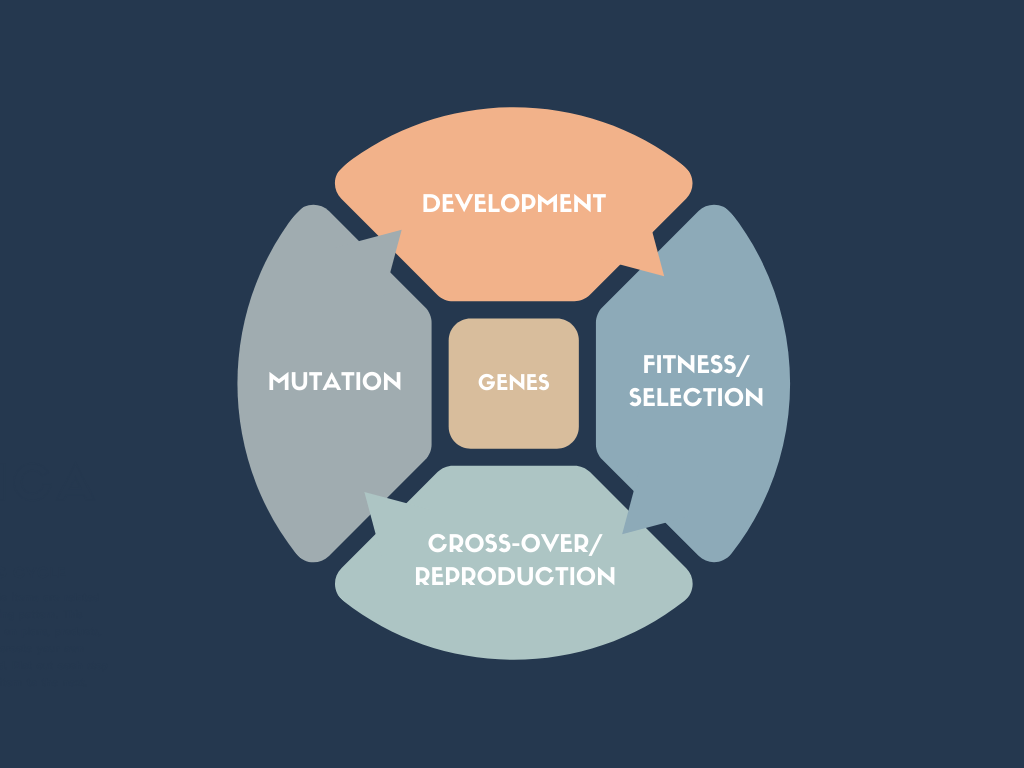
Evolution Recap¶
- An organism/individual is differentiated by its unique genetic code
- This genetic code will express itself in physical attributes
- These attributes impact the likelihood of survival
- Surviving organisms are more likely to reproduce
- Reproduction allows an organism to partially pass on their genes
- Mutations can occur at any time to change an organism's genes
Components of Evolution¶
- Genes
- Fitness/Selection
- Cross-over/Reproduction
- Mutation
Genes¶
- The smallest unit of selection
- Possible expressions of a particular gene are called alleles
- Contributes to the physical attributes of the organism
Fitness/Selection¶
- Each organism has an abstract value of fitness
- This relates to its chance of survival/reproduction
- Genes that encourage fitness are more likely to disseminate
Cross-over/Reproduction¶
- Two organisms can reproduce to have children
- Each child will take half their genetic material from each parent
- This loosely corresponds to 'mixing' the genes of the parents
Mutation¶
- Genes can mutate to change their expression
- This can occur at any time but is more likely at birth
Bringing it Together¶
Application to Optimisation¶
- Genes -> Parameters
- Fitness -> Score
- Definitions of reproduction/mutation
- No one 'correct' formulation
Example: Quadratic Regression¶
Task¶
- Find optimal (least squares) coefficents to fit noisy quadratic data
Genes¶
gene_pool = {
'a': (-3, 3),
'b': (-3, 3),
'c': (-3, 3),
}
# Initialisation
genome = {
gene: random.uniform(alleles[0], alleles[1])
for gene, alleles in population.gene_pool.items()
}
Fitness/Selection¶
self._fitness = -np.mean(np.square(y_hat - y))
ranked_organisms = sorted(self.organisms,
key=lambda org: org.fitness,
reverse=True)
survived = ranked_organisms[:self.retain_length]
for org in ranked_organisms[self.retain_length:]:
if len(survived) >= self.size:
break
if self.random_select > random.random():
survived.append(org)
# Determine how many children to create
shortfall = self.size - len(survived)
children = []
while len(children) < shortfall:
mother = random.choice(survived)
father = random.choice([s for s in survived
if s is not mother])
children.extend(
Organism.breed(mother, father,
min(2, shortfall - len(children)))
)
self.organisms = survived + children
Cross-over/Reproduction¶
for gene in mother.population.gene_pool.keys():
# Convex combination of parents' alleles
p = random.random()
genome[gene] = p * mother.genome[gene] + \
(1-p) * father.genome[gene]
Mutation¶
for gene, alleles in self.population.gene_pool.items():
if self.population.mutation_chance > random.random():
# Convex combination of current allele and random
# choice from the gene pool
p = (1 + random.random()) / 2
self.genome[gene] = p * self.genome[gene] + \
(1-p) * random.uniform(alleles[0], alleles[1])
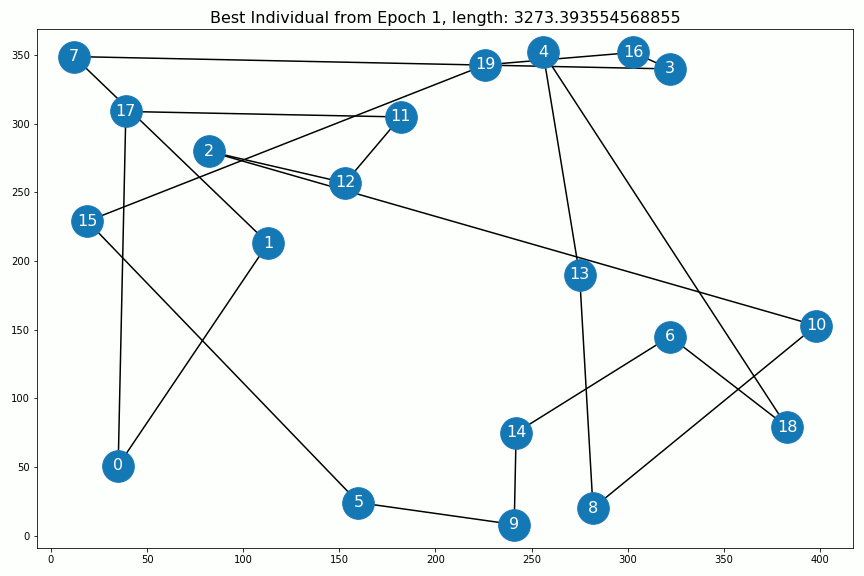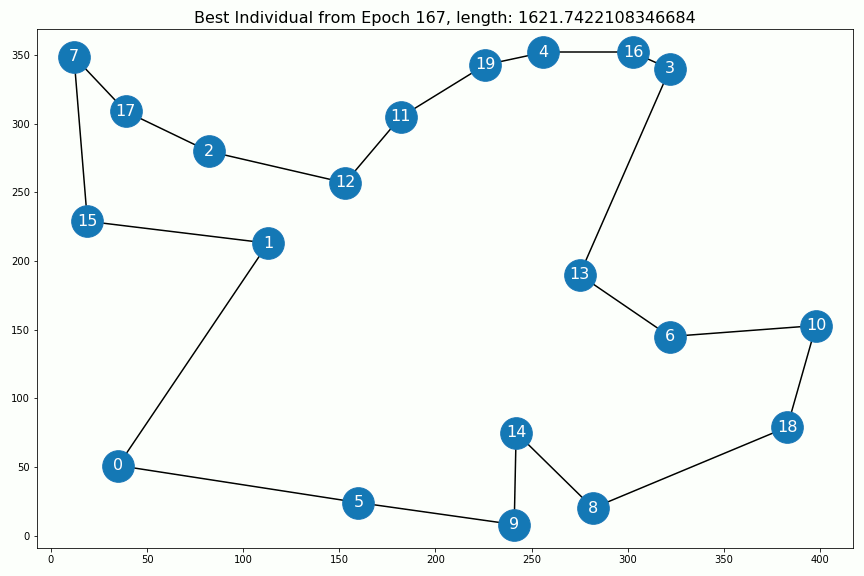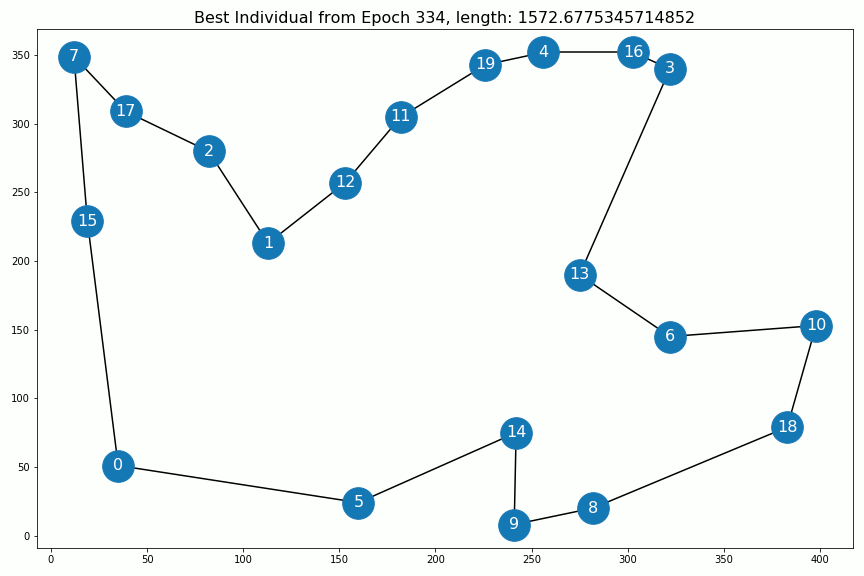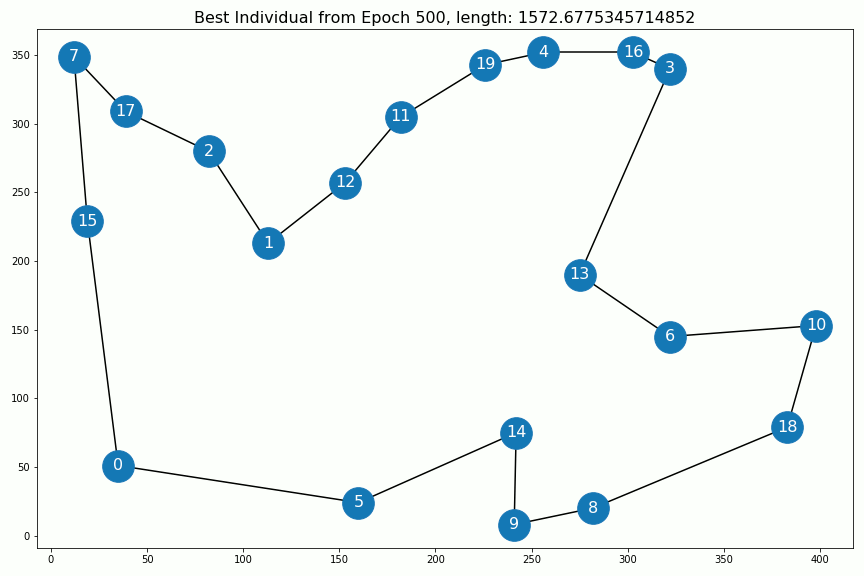
Results¶
Out[5]:
Out[6]:
Comparison to Grid Search¶
- Grid search on integer lattice: $7^3=343$ combinations
- For precision of $0.5$ this increases to $13^3=2197$
- Evolutionary method above had $20$ organisms per generation
- Linear in number of generations
- Reasonable convergence at $5$ generations
Comparison to Gradient Descent¶
$$
\begin{align}
\sum\left(y-\hat{y}'\right)^2 &:= \sum\left(y-\hat{y} + c - \hat{c}\right)^2 \\ &= \sum\left[\left(y-\hat{y}\right)^2 + \left(y-\hat{y}\right)\left(c - \hat{c}\right) + \left(c-\hat{c}\right)^2\right] \\ &= \sum\left(y-\hat{y}\right)^2 + K \qquad \left[\sum\left(y-\hat{y}\right)=0\right]
\end{align}$$
Key point: How easy is it to calculate gradients?
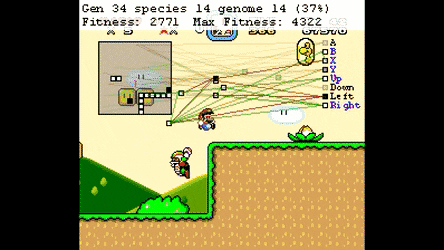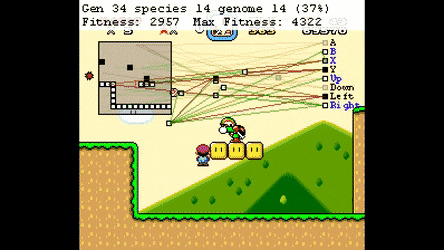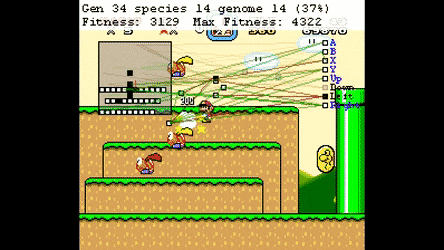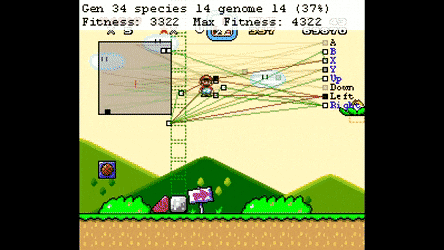
Evolutionary Algorthms in the Wild¶
Neural Networks¶
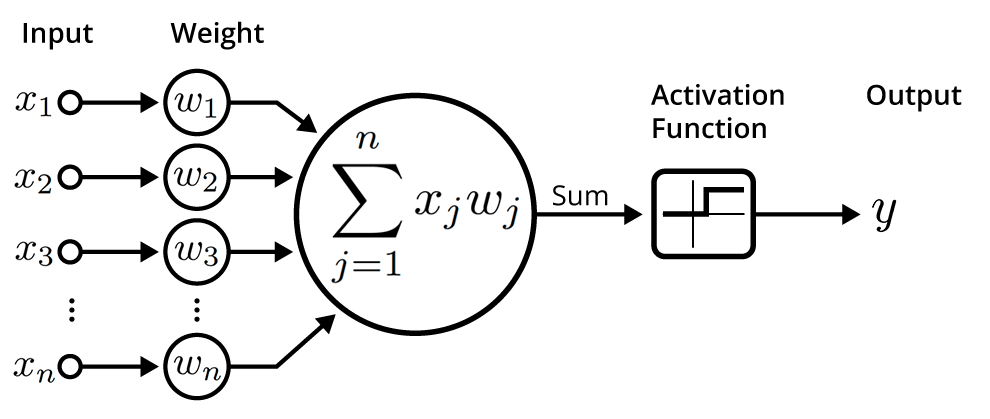
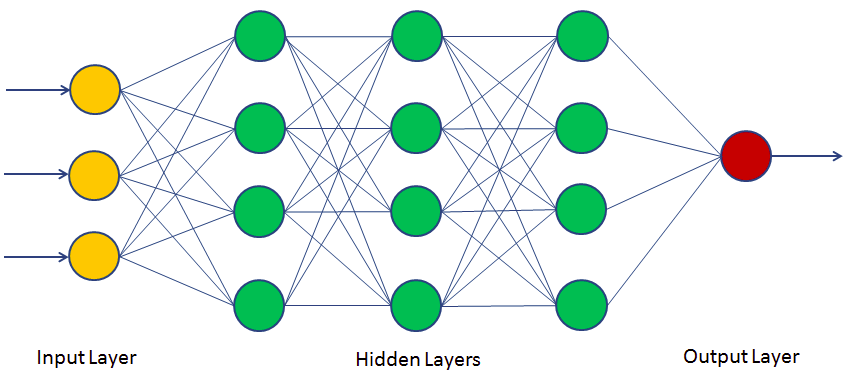
Neural Network Recap¶
- Loosely modelled on the architecture of the brain
- Capture complex interations between inputs
Hyperparameters¶
- Learning rate?
- Batch size?
- Weight/bias initialisation?
- Which optimiser?
Neuroevolution¶
Optimisation Space¶
- Number of layers
- Number of neurons per layer
- Whether to include bias
- Whether to use dropout/how much
- Activation types
- Optimiser
Search space size: ~10000 combinations
Genes¶
gene_pool = {
'num_neurons': [32, 64, 128, 256, 512, 768, 1024],
'num_layers': [1, 2, 3, 4, 5],
'use_bias': [True, False],
'dropout_rate': [0., .1, .2, .3, .4],
'activation': ['relu', 'elu', 'tanh', 'sigmoid'],
'optimiser': ['rmsprop', 'adam', 'sgd', 'adagrad',
'adadelta', 'adamax', 'nadam'],
}
# Initialisation
genome = {
gene: random.choice(alleles)
for gene, alleles in population.gene_pool.items()
}
Fitness/Selection¶
self._fitness = self.train_and_evaluate()
def train_and_evaluate(self):
"""Train this organism's model and report the final accuarcy."""
if self.population.verbose:
print(f"Training model {self.id}")
# For prototype, only train for one epoch
self.model.fit(X_train, y_train,
batch_size=1024,
epochs=1,
verbose=False,
validation_data=(X_test, y_test))
score = self.model.evaluate(X_test, y_test, verbose=False)
return score[1] # accuracy
ranked_organisms = sorted(self.organisms,
key=lambda org: org.fitness,
reverse=True)
survived = ranked_organisms[:self.retain_length]
for org in ranked_organisms[self.retain_length:]:
if len(survived) >= self.size:
break
if self.random_select > random.random():
survived.append(org)
# Determine how many children to create
shortfall = self.size - len(survived)
children = []
while len(children) < shortfall:
mother = random.choice(survived)
father = random.choice([s for s in survived
if s is not mother])
children.extend(
Organism.breed(mother, father,
min(2, shortfall - len(children)))
)
self.organisms = survived + children
Cross-over/Reproduction¶
for gene in mother.population.gene_pool.keys():
genome[gene] = random.choice((
mother.genome[gene], father.genome[gene]
))
Mutation¶
for gene, alleles in self.population.gene_pool.items():
if self.population.mutation_chance > random.random():
self.genome[gene] = random.choice(alleles)
Results¶
Out[16]:
Comparison to Random Search¶
Conclusion¶
Where next?¶
- Productionising solution
- Experimenting with different selection/reproduction/mutation techniques
- Parallel training on multiple GPUs
- More sophisticated initialisation
Wrapping Up¶
- Source material/presentation: https://github.com/THargreaves/neuroevolution-talk
- Thank you for listening
- Any questions?